

Sistemas Analógicos e Digitais
Sistemas físicos usam grandezas que são representadas e processadas aritmeticamente.
As grandezas ou quantidades podem ser representadas numericamente na forma analógica ou na forma discreta.
Quantidades discretas - entre dois valores, existe um número finito de valores e variam passo a passo.
Representação Digital - uma quantidade é representada por um arranjo de símbolos chamados dígitos.
Analógica = Contínua
Digital = Discreta
Sistemas Analógicos e Digitais
Sistema Digital - combinação de dispositivos projetado para manipular grandezas físicas ou informação que são representadas na forma digital, que só podem assumir valôres discretos.
Sistema Analógico - contém dispositivos que manipulam grandezas físicas que são representadas na forma analógica, que podem variar em uma faixa contínua de valôres.
| - Mais Fáceis de Projetar - Facilidade de Armazenamento da Informação Digital - Maiores Precisão e Exatidão - Operação Programada - Menos Suscetível a Ruídos - Maior Integração dos Circuitos Integrados(CIs) |
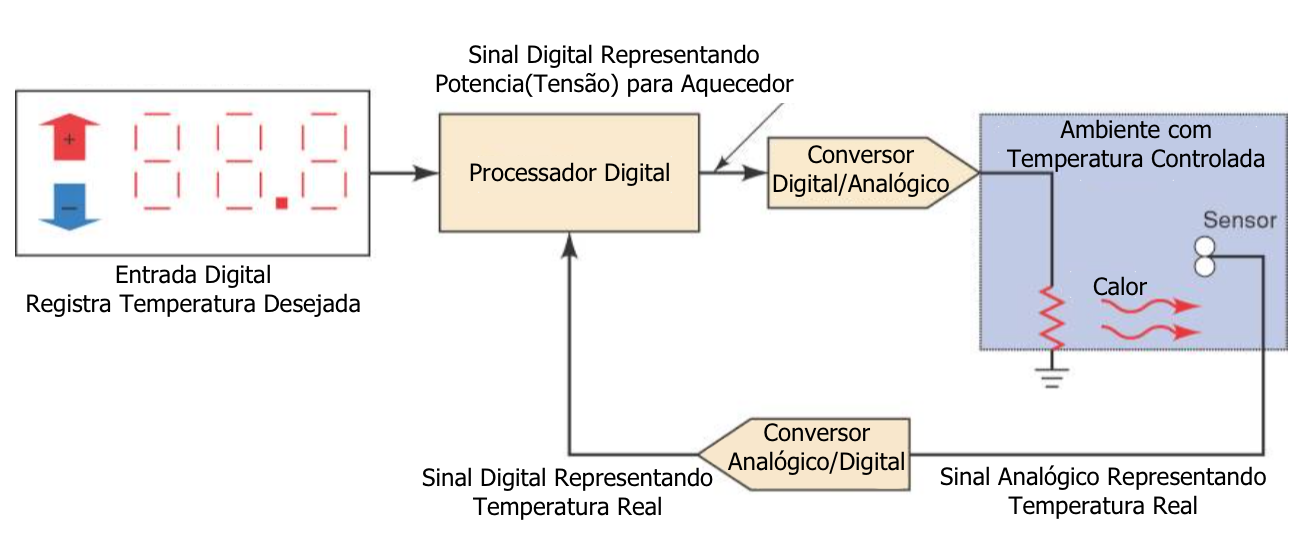
A natureza analógica de grandezas físicas naturais requer tempo para processar sinais digitais. Os passos a serem seguidos são os seguintes:
1. Converter a variável física em um sinal elétrico analógico.
2. Converter as entradas elétricas analógicas do mundo real no formato digital.
3. Realizar o processamento(operação) da informação digital.
4. Converter as saídas digitais de volta ao formato analógico(formato do mundo real).
Variáveis e Funções Lógicas
Variável - letra ou símbolo que pode assumir qualquer valor equivalente a um número de um conjunto de números, quando o conjunto contém mais de um número.
Campo de uma Variável - intervalo de valôres que pode ser assumido por uma variável.
Função - regra(relação) da qual se determina o valor de uma segunda variável (dependente) do valor da variável independente
Variáveis Lógicas
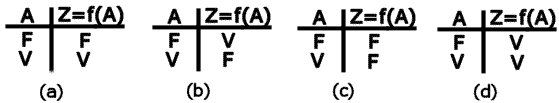 |
Nas tabelas verdades (c) e (d), os valôres de Z independem dos valôres assumidos por A.
Funções de Duas Variáveis Lógicas
Função AND(E):
Z=f(A,B) somente é verdadeira quando A e B são ambas verdadeiras.
A tabela verdade da função AND(E) é mostrada na Fig.2.
| Tabela Verdade | Representação | Propriedades |
|
||||||||||||||||||||
|
|
|
|||||||||||||||||||||
| Fig.2 |
|
||||||||||||||||||||||
Função OR(OU):
Z=f(A,B) somente é verdadeira quando uma das variáveis ou ambas são verdadeiras.
A tabela verdade da função OR(OU) é mostrada na Fig.3.
|
Fig.3 |
|
Representação de Variáveis Lógicas por Tensões Elétricas
Em geral, usa-se uma faixa de tensão para representar o valor falso ou verdadeiro de uma variável lógica.
Lógica Positiva - a tensão mais positiva representa o valor V e a mais negativa o valor F.
Lógica Negativa - o valor V é representado pela tensão mais negativa e F pela tensão mais positiva.
Lógica Mista - no mesmo sistema, usa-se as lógicas positiva e negativa.
Porta Lógica - estrutura que gera uma função lógica Z.
Símbolos
A Fig.4 mostra os símbolos lógicos para as portas lógicas OU(OR) e E(AND).
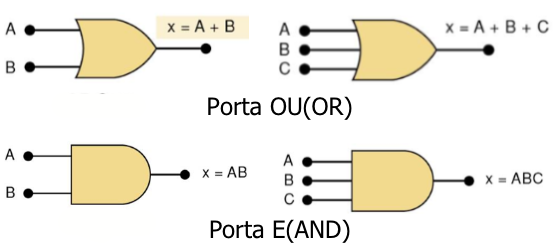 |
Inversão - Função NOT(NÃO)
Inversor - porta lógica com uma única entrada e uma única saída, que é a inversão lógica(complemento) da entrada.
A Fig.5 mosta o símbolo lógico da porta INVERSOR e o emprego em outras estruturas.
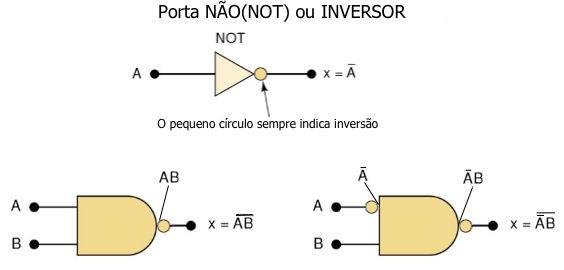
Os símbolos das portas lógicas apresentados são os símbolos usados pela maioria dos livros e indústria. Esta simbologia útil para representar portas lógicas não funciona adequadamente para CIs complexos com várias entradas e saídas.
A norma técnica IEEE/ANSI 91-1984 padronizou um novo conjunto de símbolos lógicos e a notação de dependência para CIs. A Fig.5 mostra os novos símbolos.
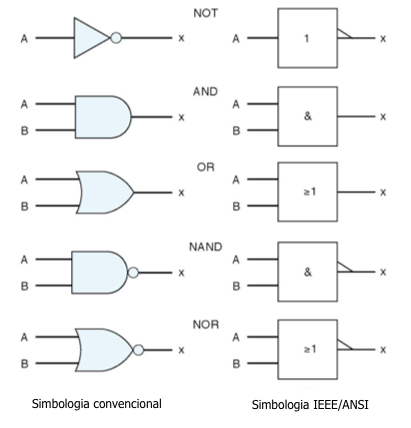 |
Fig.5b |
Notação 0 e 1
Para uma variável lógica com valor VERDADEIRO(V) emprega-se A=1 e para valor FALSO(F) da variável lógica A, usa-se A=0.
Observe que 0 e 1 não são números, mas valores lógicos de uma variável lógica. Então, as funções AND e OR ficam com as seguintes tabelas verdades:
| Função AND: | Função OR: |
|
||||||||||||||||||||||||||||||
|
|
Álgebra de Boole
Teoremas da Álgebra de Boole
Princípio da Dualidade - em uma equação lógica, se trocar (+) por (.), (.) por (+), 0s por 1s, e 1s por 0s, então substitui-se a equação original por outra igualmente válida.
Teoremas Duais - teoremas obtidos trocando as operações (+) por (.), (.) por (+) e 0s por 1s, 1s por 0s; as expressões derivadas são chamadas duais uma da outra.
| Teoremas | ||||||
| I. O complemento do complemento de uma variável lógica A é a própria variável A. |
||||||
| Fig.6 |
||||||
| II. Teoremas de uma única variável. |
III.Teoremas de duas e três variáveis sob a forma de pares duais. |
|||||
|
|
Fig.7 | ||||
![]()
Fig.9a
(2) o complemento de uma soma de variáveis é igual ao produto dos complementos de cada uma das variáveis.
![]()
Fig.9b
As Funções de Duas Variáveis
Existem dezesseis funções de duas variáveis, das quais examinamos acima as funções AND, OR e
NOT.
Agora examinaremos as funções restantes, particularmente aquelas que interessam à eletrônica digital.
A tabela abaixo mostra todas as dezesseis funções, com destaque para aquelas de interesse.
| Função | |||||
| f=0 | |||||
| f=A AND B | |||||
| f=A NOT-IMPLIES B | |||||
| f=A | |||||
| f=B NOT-IMPLIES A | |||||
| f=B | |||||
| f=A X-OR B | |||||
| f=A OR B | |||||
| f=A NOR B | |||||
| f=A X-NOR B | |||||
| f=NOT B | |||||
| f=B IMPLIES A | |||||
| f=NOT A | |||||
| f=A IMPLIES B | |||||
| f=A NAND B | |||||
| f=1 |
A Função EXCLUSIVE-OR(X-OR)
A função EXCLUSIVE-OR(OU-EXCLUSIVO), f6, fornece saída igual a valor lógico 1 se uma das variáveis de entrada A ou B, na exclusão da outra variável, tiver valor lógico 1.
| Tabela Verdade | Representação | Propriedades | ||||||||||||||||||
|
|
Símbolo da porta lógica X-OR
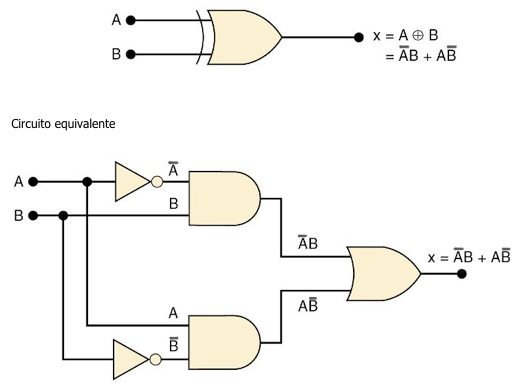
Fig.11
A Função EXCLUSIVE-NOR(X-NOR)
A função EXCLUSIVE-NOR(NOR-EXCLUSIVO), f9, fornece saída igual a valor lógico 1 se as duas variáveis de entrada A e B tiverem valores lógicos iguais. Esta função é também chamada função EQUIVALÊNCIA .
| Tabela Verdade | Representação | Propriedades | ||||||||||||||||||
|
Símbolo da porta lógica X-NOR
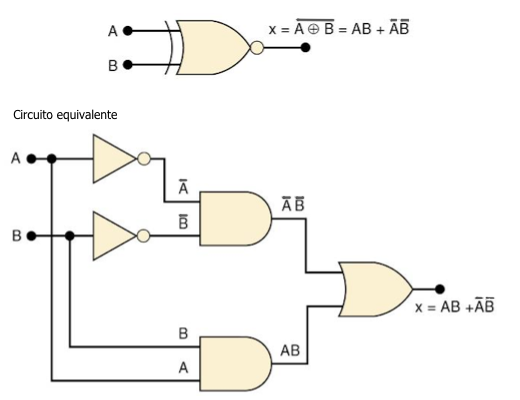 :
:
Fig.12
As Funções NAND e NOR
A Função NAND
Z=f(A,B) = A NAND B somente é 0 quando A e B são ambas iguais a 1.
A tabela verdade da função NAND é mostrada abaixo.
| Tabela Verdade | Representação | Propriedades |
|
||||||||||||||||||
|
|
Símbolo da porta lógica NAND
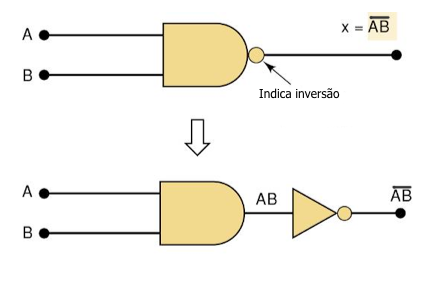
A Função NOR
Z=f(A,B) = A NOR B somente é 1 quando A e B são ambas iguais a 0.
A tabela verdade da função NOR é mostrada abaixo:
| Tabela Verdade | Representação | Propriedades |
|
||||||||||||||||||
|
|
Símbolo da Porta Lógica NOR
| Questões para Revisão - Funções lógicas NAND e NOR. Resolva essas questões sobre as funções NAND e NOR. |
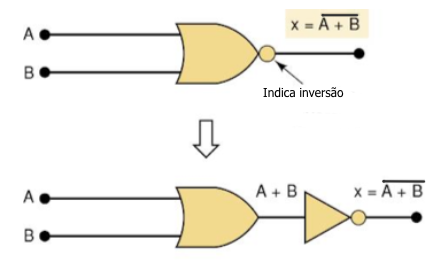
Representação Alternativa das Portas Lógicas
Regras para obter a representação alternativa das portas lógicas:
1. Inverta cada entrada e saída do símbolo padrão da porta lógica
2. Trocar todas as operações AND por OR e, todas as operações OR por AND;
3. O símbolo da operação INVERSOR permanece inalterado.
A Fig.13 mostra os símbolos padrões de representação das portas lógicas e as correspondentes representações alternativas.
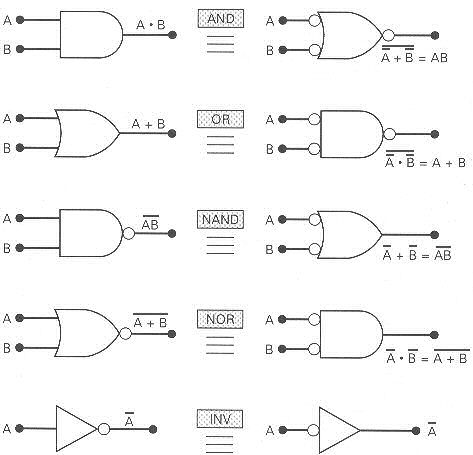
Fig.13
Algumas propriedades podem ser observadas nas representações das portas lógicas:
a) a equivalência pode ser estendida para portas com qualquer número de entradas;
b) nenhum símbolo padrão tem inversão na entrada; todos os símbolos alternativos tem inversão na entrada;
c) os símbolos padrão e alternativo de cada porta representam o mesmo circuito físico; não há diferenças no circuito representado pelos dois símbolos;
d) NAND e NOR são portas inversoras, assim os símbolos lógicos padrão e alternativo tem inversores na saída, ou na entrada; AND e OR são portas não inversoras, assim os símbolos lógicos padrão e alternativo tem inversores na entrada e saída.
Para determinar o símbolo lógico alternativo para uma porta lógica, no símbolo lógico padrão troque as operações OR por AND, ou AND por OR, e substitua as inversões nas entradas e saídas (apague as inversões onde existem e acrescente onde não existem).
Interpretação do Símbolo Lógico
Nível lógico ATIVO ALTO - quando a linha de entrada ou saída do símbolo lógico de um circuito lógico não tem inversão.
Nível lógico ATIVO BAIXO - quando uma linha de entrada ou saída do símbolo de um circuito lógico tem inversão.
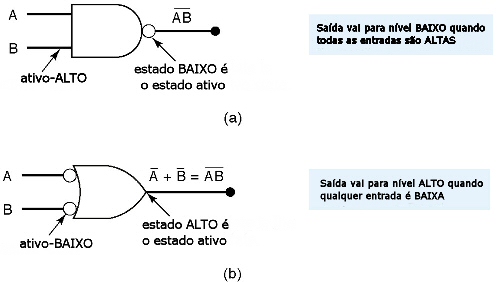
Fig.14
Para determinar os níveis lógicos ATIVOS para as entradas e saídas de uma porta lógica, basta observar que se símbolo lógico AND é usado, então a saída é ATIVA se todas as entradas são ATIVAS; se um símbolo OR é usado, então a saída é ATIVA se qualquer entrada é ATIVA.
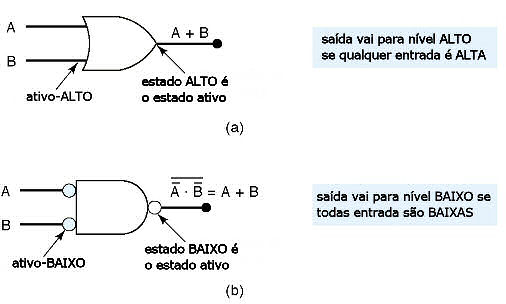
Fig.15
Suficiência das Operações NAND e NOR
A operação NOT, juntamente com a operação AND ou juntamente com a operação OR, é suficiente para expressar qualquer função lógica.
Esta propriedade é consequência direta da relação entre as funções de duas variáveis e as funções NOT, AND e OR, que podem expressar qualquer outra função.
Suficiência de NAND
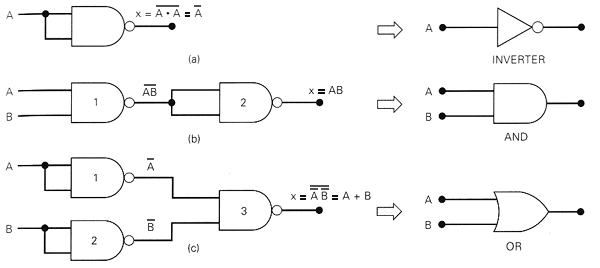
Fig.17
Suficiência de NOR
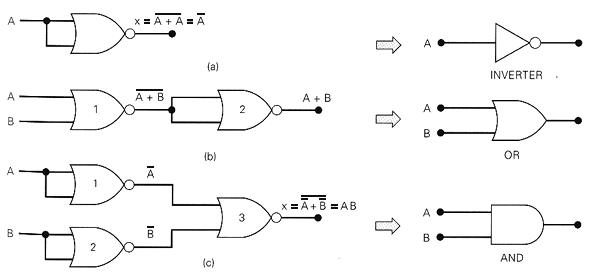
Fig.18
Questões para Revisão - Álgebra das Variáveis Lógicas e Teoremas de Boole |

Atualizada em 27/02/25
