

Quando o nível lógico de saída de um circuito lógico é dado para todas as combinações possíveis das entradas, então o resultado pode ser colocado em uma tabela verdade.
A equação do circuito pode ser derivada da tabela verdade considerando que as linhas da tabela verdade que apresentam saídas no nível lógico 1 correspondem a mintermos que participam da função expressa como soma padrão de produtos.
Após obtida a equação da função deve-se proceder a simplificação e, em seguida, implementar o circuito. Os passos a serem seguidos para projetar um circuito lógico com este método são os seguintes:
Exemplo
Projetar um circuito lógico que tem três entradas A, B e C e uma saída x que será ALTA somente quando a maioria das entradas é ALTA.
O problema estabelece que a saída x será 1 quando duas ou mais entradas sejam iguais a 1; para todos outros casos a saída x será igual a 0
| Mintermo | |||||
Existem quatro linhas cujas saídas são iguais ao nível lógico 1: linhas 3, 5, 6, e 7. Os mintermos estão indicados nas linhas correspondentes. Observe que o número dos mintermos é igual ao número da linha.
Escrevendo a expressão OR para os termos AND indicados na tabela verdade, temos:
| Equação original do circuito | |
| Somando ABC a outros termos | |
| Fatorando os pares de termos | |
| Termos entre parênteses são 1 | |
| Eliminando os parênteses | |
| Equação simplificada |
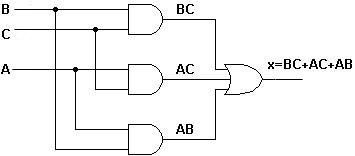
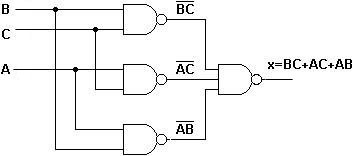
Fig.2
Simplificação de Circuitos Lógicos
Uma vez obtida a equação do circuito lógico, a partir da tabela verdade, pode-se reduzir a expressão obtida a uma forma mais simples, com um número menor de termos ou de variáveis, em um ou mais termos. A expressão simplificada pode ser usada para implementar o circuito que é equivalente ao circuito original mas tem menos portas e conexões.
 |
Os métodos de simplificação de funções lógicas existentes são os seguintes:
Este método de simplificação usa as equações e teoremas de Boole e DeMorgan. Não existe uma regra que indique quais teoremas devem ser utilizados para simplificar uma determinada equação. Também não há uma maneira de ter a certeza que a expressão obtida é a mais simples ou se comporta outras simplificaçães. Então este método é um processo de tentativas e erros, onde prática e experiência são importantes para se obter bons resultados.
Para aplicar o método algébrico na simplificação de equações lógicas deve-se empregar dois passos básicos:
Exemplo
Simplificação da equação do circuito da Fig.4 é realizada abaixo:
| Equação original do circuito | |
| Aplicando teorema 17 | |
| Cancelando dupla inversão | |
| Eliminando parênteses | |
| A AND A é A | |
| B OR NOT B é 1 | |
| AC AND 1 é AC | |
| Fatorando A | |
| Equação simplificada |
A Fig.5 abaixo mostra um circuito lógico com duas entradas A e B e uma saída z. A simplificação de z está em seguida.
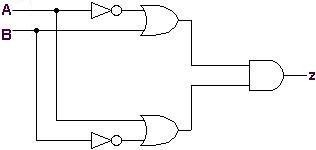 |
Simplificação:
|
||||||||||
Fig.5 |
|||||||||||
| Circuito simplificado: | |||||||||||
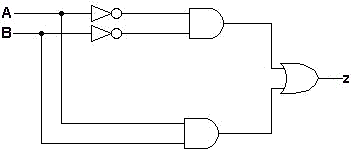 |
|||||||||||
Fig.6 |
|||||||||||
O circuito está implementado na Fig.3 e comparando com o circuito original vemos que o circuito tem o mesmo número de portas e de conexões. A simplificação produziu um circuito equivalente mas não um circuito mais simples.
Regras para Avaliar Expressões Lógicas
1.Calcular todas as inversões de termos simples;
2.Calcular todas as expressões dentro de parênteses;
3.Calcular operações AND antes de OR, a menos que um parêntese indique o contrário;
4.Se uma expressão está complementada, então calcule a expressão primeiro e, em seguida, inverta o resultado.

|
Questões para Revisão Resolva as questões sobre simplificação e projetos de funções lógicas com estruturas de dois níveis de portas. |

Atualizada em 12/03/25
