Aluno:_____________________________________________________CPF Nº:_____________

1.Para contador da Fig.1 abaixo, desenhe as formas de onda dos sinais de saída solicitados na figura durante 12 ciclos de clock. Considere que os FFs estão inicialmente com a representação binária do segundo menor dígito de seu CPF.
a) Qual o módulo do contador?
b) Quais são os estados válidos( valores de CBA) do contador?
Solução

a) Observe que os flip-flops A e B formam um contador módulo 3 com estados de contagem iguais a

BA=00→01→10→00→...

pois quando, em curto intervalo de tempo, BA=11, os flip-flops A e B são reset, desde que as entradas CLR são colocadas em 0 pela saída da porta NAND cujas entradas são BA=11.

Agora, veja que o flip-flop C é um contador módulo 2 com estados de contagem iguais

C=0→1→0...

Então, os flip-flos C, B e A formam um contador assíncrono com módulo igual a 6.

b)Então, do exposto acima, os estados de contagem do contador CBA são iguais a

CBA=000→001→010→100→101→110→000→...

As formas de onda para A, B, e C estão mostradas abaixo e as resposta corretas correspondentes para o complemento de A e complemento de B.

Fig.1

Item a) correto = 1,0
Item b) correto = 1,0
Cada forma de onda correta = 1,0
Valor da questão = 5,0

2.Desenhe o circuito de um somador-inteiro(full adder) cujas entradas são A_i, B_i e C_i, e as saídas S_i(bit soma) e C_i+1(bit de vai-um). Use somente circuitos meio-somador(half adder) mostrado na Fig.2 e uma porta OR. Use menor quantidade possível de meio somador.
Solução

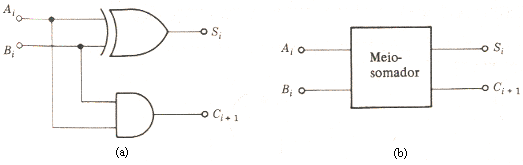
Fig.2

Sejam S_i' e C_i+1' as saídas do circuito meio-somador acima, então temos:

S'_i = A_i⊕B_i

C'_i+1 = A_iB_i

As saídas S_i e C_i+1 para um circuito somador inteiro(full adder) são dados pelas equações abaixo:

S_i = A_i⊕B_i⊕C_i

C_i+1= A_iB_i+A_iC_i+B_iC_i

Então, substituindo o valor de S'_i = A_i⊕B_i na equação de S_i = A_i⊕B_i⊕C_i, obtemos a equação de saída do bit soma S_i para o somador inteiro que é igual a

S_i = A_i⊕B_i⊕C_i ∴ S'_i = A_i⊕B_i ∴ S_i =S'_i⊕C_i

Então, para realizar a soma de A_i, B_i e C_i serão necessários dois meio somadores, na configuração abaixo:

Fig.3

Observe que o primeiro meio somador fornece o vai-um C'_i+1 e o segundo meio somador fornece o vai-um C"_i+1 dados pelas equações abaixo:

C'_i+1 = A_iB_i e C"_i+1 = S'_iC_i

Como S'_i = A_i⊕B_i, então C"_i+1 é dado ela equação abaixo:

C"_i+1 = (A_i⊕B_i)C_i

O bit de vai-um da soma de A_i, B_i e C_i é dado pela equação abaixo:

E o circuito completo do somador inteiro com dois meio somadores e uma porta OR é mostrado na Fig.4 abaixo:

Fig.4

Circuito do somador inteiro correto = 3,0
Equação de C_i+1(bit de vai-um) correta = 1,0
Equação de S_i(bit soma) correta = 1,0
Valor da questão = 5,0