Eletrônica Digital - Uso dos Mapas K

barra_de_navegacao

Uso dos Mapas K

Regras Para Simplificar Funções Lógicas Na Forma Padrão de Soma de Produtos

(1)A combinação de quadrículos(mintermos) deve incluir todos os quadrículos pelo menos uma vez(o mesmo quadrículo pode aparecer em mais de uma combinação).

(2)As combinações devem incluir o maior número possível de quadrículos, de modo que todos os quadrículos sejam incluídos pelo menor número possível de combinações.

Produtos ou Implicantes Primos - são as combinações de quadrículos.

Implicante Primo Essencial - é o implicante que deve necessariamente constar na combinação.

A cada implicante primo corresponde uma porta AND.

O número de entradas da porta AND diminui com o aumento do número de quadrículos incluídos na combinação.

Existem dois critérios para se determinar a economia de um circuito:

(1) Circuito com menor quantidade de portas.

(2) Circuitos com o mesmo número de portas, então o mais econômico tem o menor número de entradas.

Algoritmo Para Obtenção da Expressão Mínima de Uma Função

(1)Assinalar e considerar como implicante primo essencial qualquer quadrículo que não possa ser combinado com nenhum outro.

(2)Identificar os quadrículos que podem se combinados com um único outro quadrículo somente de uma maneira; assinalar estas combinações.

(3)Identificar quadrículos que podem ser combinados com três outros quadrículos somente de uma maneira; se os quadrículos de tais combinações ainda não estiverem incluídos em grupos de dois, assinalar a combinação de quatro.

(4) Repetir o processo para grupo de oito, etc...

(5) Se ainda restarem alguns quadrículos não incluídos em grupamentos, podem ser combinados uns com os outros ou com quadrículos incluídos em outros grupamentos.

Exemplo. Simplificar a função

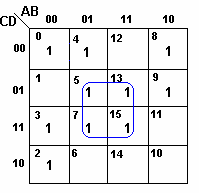Fig.1	Fig.2	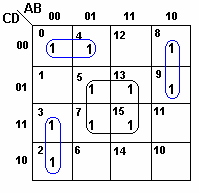Fig.3
(a)Não há implicante primo essencial (b)Não há quadrículos que possam ser combinados de uma única maneira com outros quadrículos.	(c)os mintermos m₅, m₇, m₁₃, m₁₅ podem ser agrupados em um único grupo de quatro.	(d)Os quadrículos restantes podem ser agrupados arbitrariamente.
Então, a função simplificada é dada por


Exemplo. Simplificar a função SOP

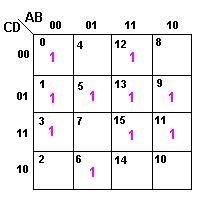Fig.4	(a)m₆ é implicante primo essencial. (b)m₀ e m₁₂ só podem ser combinados em grupos de dois de uma única maneira. (c)m₃, m₅ e m₁₅ podem ser combinados em grupos de quatro somente de uma maneira e os grupos de quatro incluem quadrículos ainda não incorporados a grupos de dois. (d)agrupando todas as combinações vemos que todos os quadrículos foram incluídos.	Fig.5
A função simplificada é dada por

Simplificação de Funções Expressas com Maxtermos

Implicado Primo é o termo soma em um produto de somas.

Vejamos a simplificação da função POS cujo mapeamento é dado abaixo.

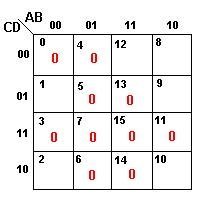Fig.6	(a)Não há nenhum implicado primo essencial (b)M₀ só pode se combinar de uma única maneira com M₄ (c)M₃, M₁₃ e M₁₄ só podem ser combinados com três outros de uma única maneira (d)Não há nenhum grupo de oito possível (e)Agrupando todas as combinações vemos que todos os quadrículos estão em alguma combinação.
Então, os termos soma são dados por	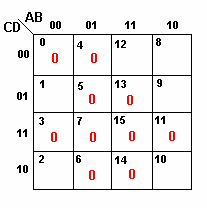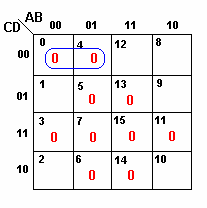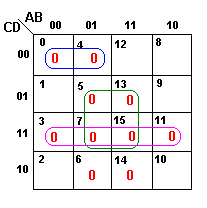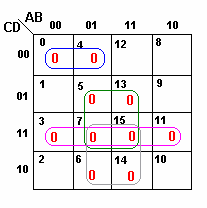Fig.7
E a função simplificada é igual a

Estrutura de portas
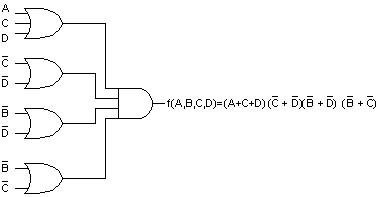Fig.8

Mapeamento de Funções Não-Padronizadas

Uma função não-padronizada para ser mapeada e simplificada usando mapa K deve ser expressa como soma de mintermos ou produto de maxtermos.

Vamos mapear e simplificar a função dada pela equação lógica abaixo.

(a)O termo pode ser mapeado diretamente no mapa K

(b)O termo está nos intervalos B e D, fora do intervalo C e independe de A

(c)O termo está fora dos intervalos A e C e independe de B e D

(d)O termo está no intervalo A e independe de B, C, e D

fig23

Fig.11

(a) Implicante primo essencial: não há

(b) Combinação de dois quadrículos: não há

(d) Combinação de oito quadrículos

E a função será expressa como a soma dos termos acima.

Funções Incompletamente Especificadas

Combinações Não-Especificadas:

(a)Combinações que nunca ocorrem

(b)Combinações que não interessam

As combinações não-especificadas são indicadas na função como "don't care" e, no Mapa K ,são mapeadas com X.
Na simplificação da função, pode-se fazer X=0 ou X=1 de modo a obter a expressão mais simples da função.

Exemplo.



	Fig.12
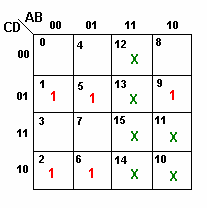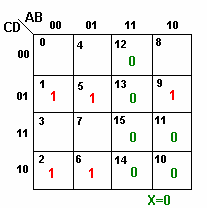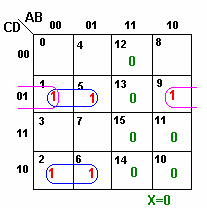
Considerando os valores X iguais a 0, a função simplificada é igual a



Fig.13
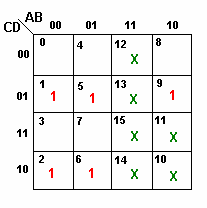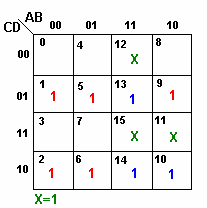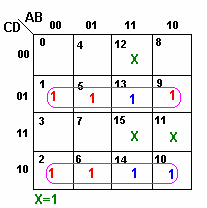
Considerando X=1 nas posições que simplificam a função:

Questões para Revisão
Resolva as questões e problemas propostos por esse teste. Empregue o método de Mapas K e, em seguida, use os programas indicados nesta página e compare os resultados.

Atualizada em 12/03/25

apple_logo