

Mapas de Karnaugh - figura geométrica que contém uma região(quadrículo) para cada linha de uma tabela verdade.
Existe uma correspondência entre os quadrículos do Mapa de Karnaugh(Mapa K) e os mintermos e maxtermos.
O Mapa K é uma ferramenta usada para simplificar uma equação lógica ou para converter uma tabela verdade para o circuito lógico correspondente de modo ordenado e simples.
O Mapa K pode ser empregado para circuitos com qualquer número de variáveis de entrada, porém sua utilidade prática é limitada a cinco ou seis variáveis.
Mapa K Para Uma Variável\
A tabela verdade fornece os valores da saída para cada combinação dos valores de entrada.
O Mapa K dá a mesma informação de foram diferente. Cada linha da tabela verdade corresponde a uma quadrícula no Mapa K.
As linha da tabela verdade que apresentam saídas iguais a 1(ou 0), correspondem a quadrículas que são preenchidas com 1(ou 0).
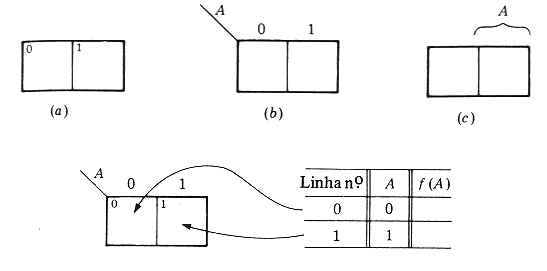 |
A forma do Mapa K depende exclusivamente do número de variáveis incluídas, e não da expressão booleana para a qual o mapa será usado.
Observe os três modos diferentes de representar um mapa K para uma variável apresentados na Fig.1(a), 1(b) e 1(c), e esses três modos incluídos em um único Mapa K.
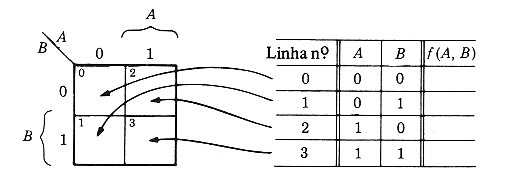
Mapa K Para Duas Variáveis
 |
Representação de Uma Função no Mapa K
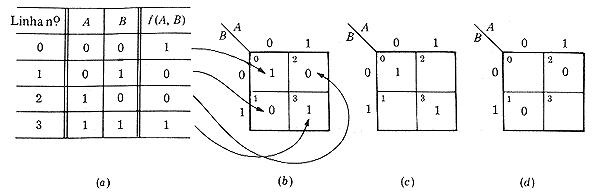 |
Veja que em (a) temos a tabela verdade da função, em (b) o mapa K correspondente com os valôres lógico da função mapeados em cada quadrículo, em (c) temos apenas os 1s mapeados e em (d) somente os 0s.
Em geral, são mapeados no mapa K somente os 1s, por exclusão, os outros quadrículos tem 0s.
Mapa K Alternativo Para Duas Variáveis
|
Observe a ordenação da numeração dos quadrículos: |
||
Fig.4 |
|||
| Mapa K Para Três Variáveis | Mapa K Para Quatro Variáveis |
||
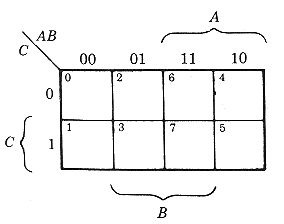 |
 |
||
| Fig.5 | Fig.6 | ||
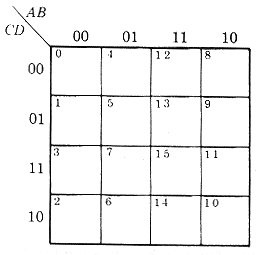
| É arbitrária a atribuição das variáveis às linhas e colunas de um mapa K e os valôres numéricos às variáveis. Exemplo:
tem número binário 1000=810 e será igual a m8.
e terá o número binário 0001=110 e será m1.O mapa K apresenta a forma da Fig.7. |
 |
|
Fig.7 |
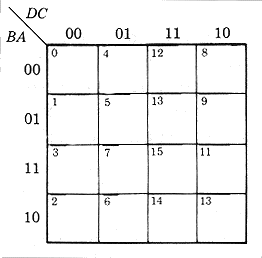
Se mantemos a variável A como a mais significativa, D como a menos siginificativa e associamos AB às linhas e CD às colunas, então a significância numérica é mantida e o mapa K apresenta a forma Fig.8. |
|
|||
Características essenciais do mapa K
Fig.9 |
Na Fig.9 ao lado, temos uma função mapeada de dois mintermos
Então, combinado os dois mintermos, teremos
|
Princípio geral
| Método alternativo | ||||||
m12 está sob a região A, então A não-complementada
m8+ m12 está sob a região A, então A não-complementada
|
Fig.10
|
|||||
 |
Questões para Revisão Resolva on-line algumas questões de revisão sobre as propriedades e construção dos Mapas de Karnaugh. |
 |
Mapas de Karnaugh Simplificar equações lógicas pelo método dos Mapas K. Visite esta página sobre Mapas de Karnaugh e pegue um programa para simplificar funções lógicas. |

Atualizada em 12/03/25
