Eletrônica Digital - Projetando Circuitos Lógicos Combinacionais

Fig.1

Os métodos de simplificação de funções lógicas existentes são os seguintes:

Método Algébrico( Algébra Booleana)
Método Gráfico(Mapas de Karnaugh)
Método Tabular(Quine-McCluskey)

O método algébrico emprega as equações e teoremas de Boole e DeMorgan, sendo intuitivo e dependente da prática; o método gráfico é sistemático, com procedimentos passo-a-passo; o método tabular é mais aplicado para simplificação usando programas específicos em microcomputadores.

Simplificação Algébrica
Este método de simplificação usa as equações e teoremas de Boole e DeMorgan. Não existe uma regra que indique quais teoremas devem ser utilizados para simplificar uma determinada equação.Também não há uma maneira de ter a certeza que a expressão obtida é a mais simples ou se comporta outras simplificaçães.Então este método é um processo de tentativas e erros, onde prática e experiência são importantes para se obter bons resultados.

Para aplicar o método algébrico na simplificação de equações lógicas deve-se empregar dois passos básicos:

A expressão original deve ser colocada na forma soma-de-produtos, pela aplicação dos teoremas de DeMorgan e multiplicação de termos.
Uma vez que a expressão está na forma soma-de-produtos, os termos produtos são verificados em busca de fatores comuns e a fatoração deve ser feita quando possível.A fatoração deve resultar na eliminação de um ou mais termos.

Como exemplo, a simplificação da equação do circuito da Figura 1 é realizada abaixo:

	Equação original do circuito

	Aplicando teorema 17

	Cancelando dupla inversão

	Eliminando parênteses

	*A AND* A é A**

	*B OR NOT* B é 1**

	*AC AND* 1 é AC**

	Fatorando A

	Equação simplificada

Fig.1

A Figura 2 abaixo mostra um circuito lógico com duas entradas A e B e uma saída z. A simplificação de z está em seguida.

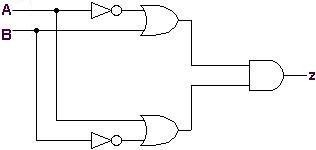Simplificação:

	Equação original do circuito

	Transformando em soma-de-produtos

Fig.2

Circuito simplificado:

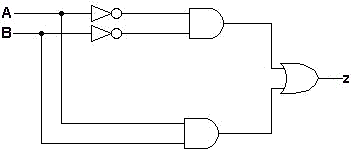Fig.3

O circuito está implementado na Fig.3 e comparando com o circuito original vemos que o circuito tem o mesmo número de portas e de conexões.A simplificação produziu um circuito equivalente mas não um circuito mais simples.

Regras para Avaliar Expressões Lógicas
1.Calcular todas as inversões de termos simples;

2.Calcular todas as expressões dentro de parênteses;

3.Calcular operações AND antes de OR, a menos que um parêntese indique o contrário;

4.Se uma expressão está complementada, então calcule a expressão primeiro e, em seguida, inverta o resultado.

Projetando Circuitos Lógicos Combinacionais
Quando o nível lógico de saída de um circuito lógico é dado para todas as combinações possíveis das entradas, então o resultado pode ser colocado em uma tabela verdade. A equação do circuito pode ser derivada da tabela verdade considerando que as linhas da tabela verdade que apresentam saídas no nível lógico 1 correspondem a mintermos que participam da função expressa como soma padrão de produtos.

Após obtida a equação da função deve-se proceder a simplificação e, em seguida, implementar o circuito.Os passos a serem seguidos para projetar um circuito lógico com este método são os seguintes:

Obter a tabela verdade
Escrever o termo AND(mintermo) para cada linha da tabela verdade cuja saída é igual ao nível lógico 1
Escrever a expressão soma-de-produtos para a equação da saída
Simplificar a expressão da equação da saída
Implementar o circuito para a expressão final simplificada.

Exemplo. Projetar um circuito lógico que tem três entradas A, B e C e uma saída x que será ALTA somente quando a maioria das entradas é ALTA.

Deduzir a tabela verdade
O problema estabelece que a saída x será 1 quando duas ou mais entradas sejam iguais a 1; para todos outros casos a saída x será igual a 0

Linha	A	B	C	x
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

Escrever os termos AND(mintermos) para cada linha da tabela verdade cuja saída é igual ao nível lógico 1
Existem quatro linhas cujas saídas são iguais ao nível lógico 1: linhas 3, 5, 6, e 7. Os mintermos estão indicados nas linhas correspondentes.Observe que o número dos mintermos é igual ao número da linha.
Determinar a expressão soma padrão de produtos para a saída x
Escrevendo a expressão OR para os termos AND indicados na tabela verdade, temos:

Simplificar a expressão da saída
A expressão da saída x será simplificada empregando os teoremas da Álgebra de Boole, conforme abaixo:

	Equação original do circuito

	*Somando ABC* a outros termos**

	Fatorando os pares de termos

	Termos entre parênteses são 1

	Eliminando os parênteses

	Equação simplificada

Implementar o circuito para a expressão final
A expressão final está na forma soma-de-produtos, então o circuito será três portas AND com uma porta OR.

Fig.4

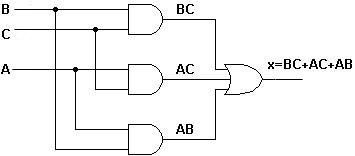
Implementando o Projeto Final
No projeto anterior o circuito final foi implementado empregando uma estrutura com portas AND e OR.Uma expressão na forma soma-de-produtos sempre fornecerá uma ou mais portas AND que acionam apenas uma porta OR.O principal motivo para usar a forma soma-de-produto é que podemos implementar o circuito emepregando somente portas NAND, sem aumentar a complexidade do circuito.

Isto pode ser feito substituindo cada porta da estrutura AND-OR obtida por portas NAND, sem fazer quaisquer outras mudanças. A Figura 5 mostra a estrutura NAND-NAND para o circuito de maioria.

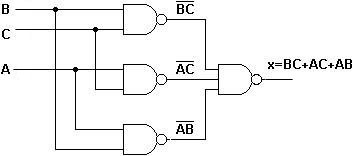
fig26
Fig.5