

Um número maior que 9 é representado usando uma convenção que atribui significado à posição ou lugar ocupado por um dígito no arranjo.
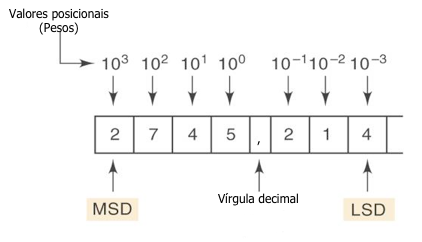
Fig.1
Exemplo.
Sistema Binário - sistema numérico de base(ou raiz) 2, que usa somente dois dígitos numéricos 0 e 1
Vantagem - correspondência biunívoca entre os dois dígitos (números) 0 e 1 e os dois valôres lógicos (não numéricos) de variáveis lógicas 0 e 1.
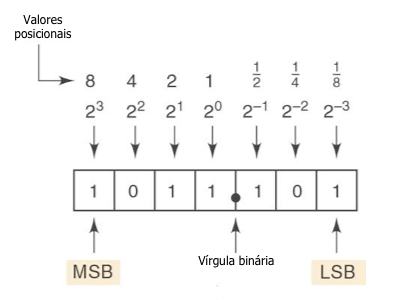
Fig.2
Exemplo.
100112 = 1X24 + 0X23 + 0X22 +1 X21 + 1X20 = 1910
1,11012 = 1X20 + 1X2-1 + 1X2-2 + 0X2-3 + 1X2-4 = 1,81210
Base: 16 |
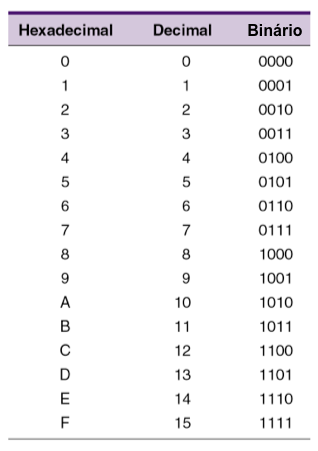 |
||
Fig.4 |
|||
Conversão entre Números Binários e Decimais
Conversão de Decimal para Binário
Converte-se a parte inteira e a parte fracionária independentemente e se justapõe os resultados.
Método das Divisões Sucessivas
A parte inteira é obtida fazendo divisões sucessivas por 2 até obter quociente igual a 0, e tomando-se os restos das divisões na ordem inversa, o primeiro resto é igual ao dígito menos significativo(LSB) e o último resto igual ao dígito mais significativo(MSB), para formar o binário equivalente.
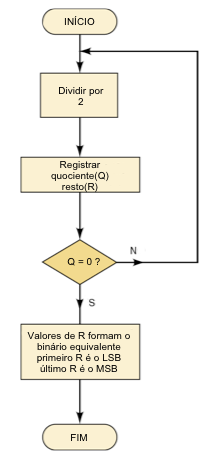
Fig.5
Exemplo.
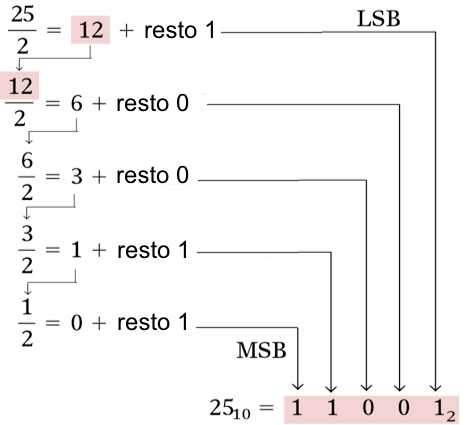
Fig.6
A parte fracionária é convertida fazendo-se multiplicação sucessivas por 2 e formando o número binário com as partes inteiras dos resultados das multiplicações.
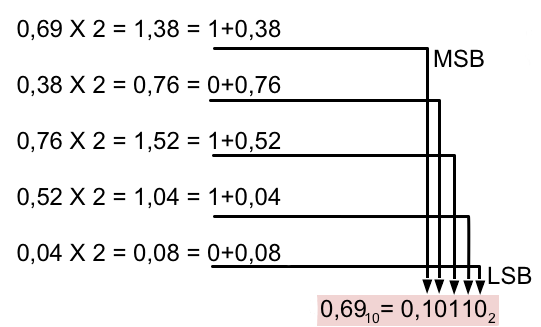
Fig.7
Então, temos o resultado abaixo.
![]()
Outro método utilizado para converter um número decimal em número binário é expressar o número decimal como uma soma de potências de 2 e, então, 1s e 0s são colocados nas posições corretas dos dígitos dentro do arranjo binário.
Exemplos.
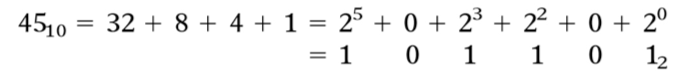
Fig.8
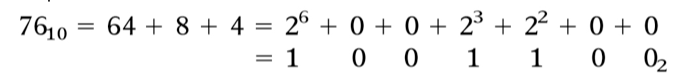
Fig.9
Conversão Binário para Decimal
Para converter um número binário para decimal deve-se multiplicar cada
dígito binário pelo seu peso no arranjo de valor posicional.
Exemplo.
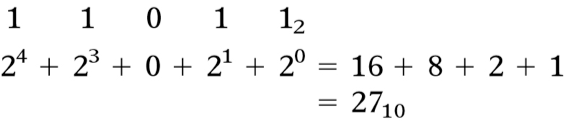
Fig.10
Exemplo.
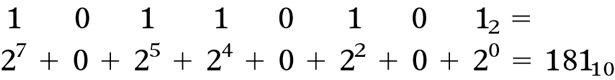
Fig.11
Conversão de Decimal para Hexadecimal
Converte-se a parte inteira e a parte fracionária independentemente e se justapõe os resultados.
Método das Divisões Sucessivas
A parte inteira é obtida fazendo divisões sucessivas por 16 até obter quociente igual a 0, e tomando-se os restos das divisões na ordem inversa, o primeiro resto é igual ao dígito menos significativo(LSB) e o último resto igual ao dígito mais significativo(MSB), para formar o hexadecimal equivalente.
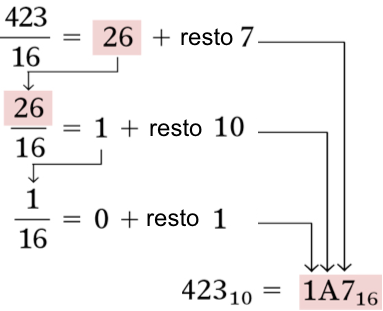
Fig.12
Conversão Hexadecimal para Decimal
Para converter um número hexadecimal para decimal deve-se multiplicar cada
dígito hexadecimal pelo seu peso no arranjo de valor posicional.
Exemplo.
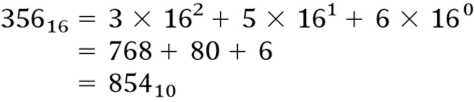
Fig.13
Exemplo. Observe que o valor de A foi substituído por 10 e o valor de F por 15.
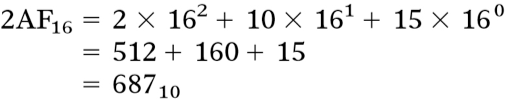
Fig.14
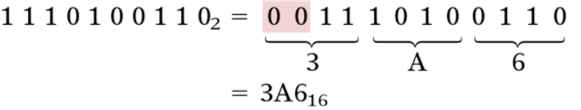
Fig.15
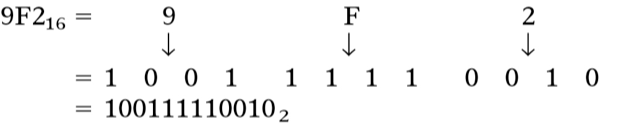
Fig.16
Códigos Numéricos BCD e Refletido(Gray)
A representação binária requer mais de três vezes o número de dígitos da representação decimal.
Na conversão, cada dígito binário afeta cada dígito decimal e vice-versa.
Decimal Codificado em Binário - BCD. No sistema BCD, quatro dígitos binários são usados para representar os dígitos decimais de 0 a 9. A tabela da Fig.17 mostra a representação BCD dos dígitos decimais.
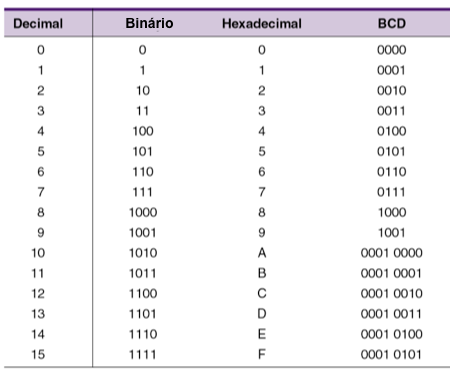
Para números decimais com mais de um dígito, a cada dígito decimal corresponde um grupo binário de 4 dígitos da correspondente representação BCD.
Exemplo.
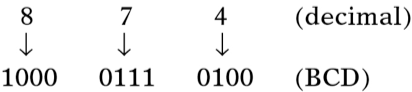
Fig.18
Para converter um número BCD para o equivalente decimal, deve-se dividir o arranjo BCD em grupos de 4 dígitos, a partir de vírgula, e substituir cada representação BCD pelo dígito decimal equivalente.
Exemplo.
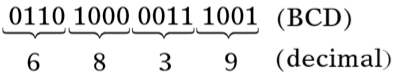
Fig.19
Desvantagem: apenas 10 das 16 combinações possíveis de quatro dígitos são utilizadas. As combinações de 10 a 15, ou seja 1010, 1011, 1100, 1101, 1110 e 1111, não são combinações válidas em BCD.
Exemplo.
![]()
Fig.20
O grupo 1100 não é uma combinação válida , um erro, em BCD, assim o arranjo é inválido em BCD e, portanto, não pode ser convertido diretamente para decimal.
Fig.20 |
O Código Refletido(Gray) é utilizado em aplicações onde os dígitos mudam muito rápido. A Fig.20 mostra a formação do Código Refletido para os números de 0 a 7 representados em binário.
Propriedades. (1) a representação de cada número difere em apenas um dígito das representações dos números imediatamente menor e maior. (2) em qualquer ponto do desenvolvimento do código, o primeiro e o último código diferem em apenas um dígito. |
Conversão de Binário para Gray e Gray para Binário
(a) o MSB em Gray é sempre igual ao MSB em Binário
(b) o próximo dígito Gray é obtido comparando-se o MSB com o segundo MSB
binários de entrada
(c) o dígito Gray seguinte
é obtido comparando-se o segundo MSB com o terceiro MSB binários de entrada
(d) ...o dígito Gray menos significativo é obtido comparando-se
o segundo LSB com o LSB binários de entrada
(e) a comparação de dígitos binários iguais gera dígito Gray igual a 0
(f)
a comparação dígitos binários diferentes resulta em dígito Gray igual a 1.
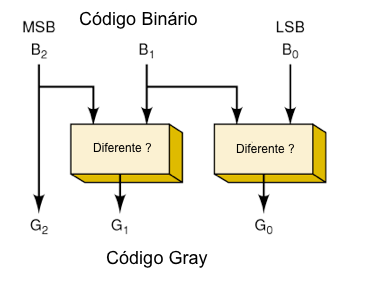
Fig.21
Conversão de Gray para Binário
(a) o MSB em Binário é sempre igual ao MSB em Gray
(b) o próximo dígito Binário é obtido comparando-se o MSB com o segundo MSB
Gray de entrada
(c) o dígito Binário seguinte
é obtido comparando-se o segundo MSB Binário de saída com o terceiro MSB Gray de entrada
(d) ...o dígito Binário menos significativo é obtido comparando-se
o segundo LSB Binário de saída com o LSB Gray de entrada
(e) a comparação de dígitos iguais gera dígito Binário igual a 0
(f)
a comparação dígitos diferentes resulta em dígito Binário igual a 1.
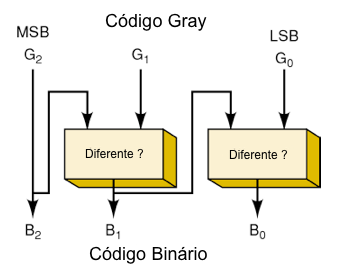
Fig.22
O Código Gray é aplicado nos codificadores ópticos, dispositivos utilizados para para converter o ângulo de rotação de um eixo mecânico em valores binários. Um codificador óptico permite a medição do ângulo de rotação de um eixo sem contato físico com o eixo.
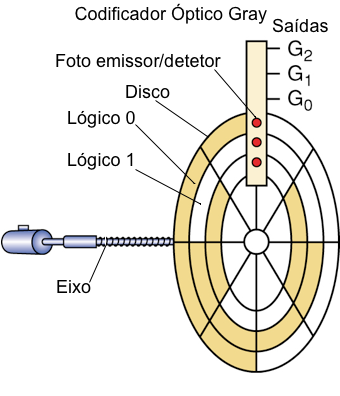
Fig.23
Representação dos Números Decimais
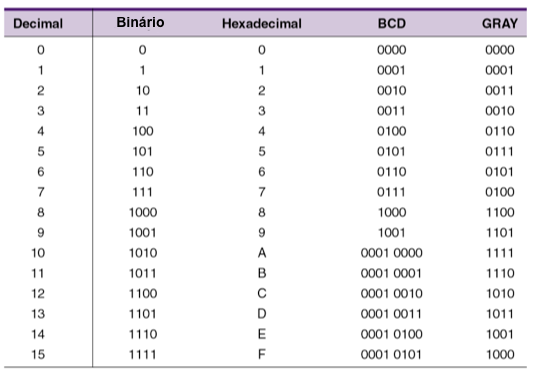
Fig.24
Códigos Alfanuméricos
Os códigos alfanuméricos såo utiizados para codificar informações que não são somente numéricas, como letras, sinais de pontuação e outros caracteres especiais.
Código ASCII
O código ASCII - American Standard Code for Information Interchange(Código Padrão Americano para Troca de Informações) - é um código de 7 bits possibilitando a codificação de 128(27) itens de informação.
O ASCII é empregado para troca de informações(dados, controle e comando) entre computadores e periféricos e é um padrão para as redes de comunicação.
A tabela da Fig.22 mostra os códigos ASCII.
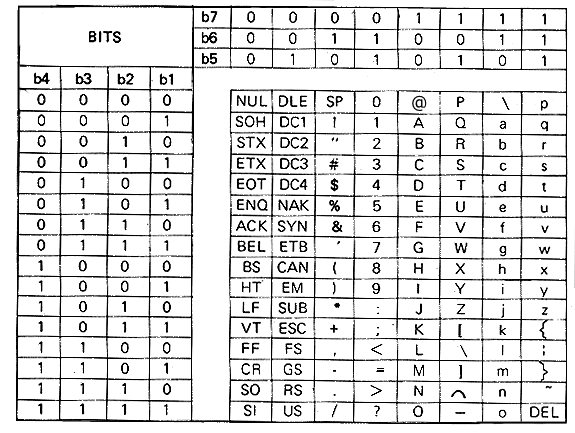
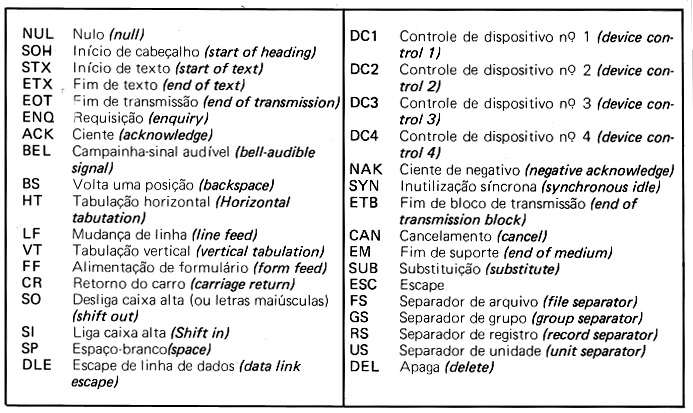
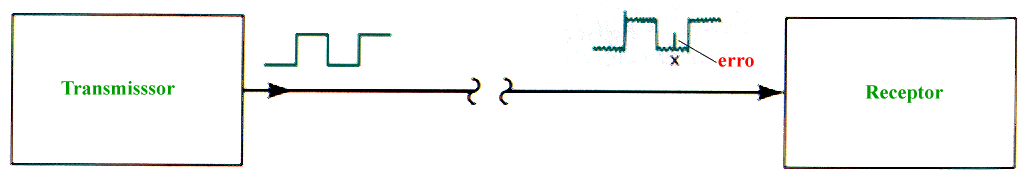
Um dos mais simples e usados métodos de deteção e correção de erros é o método da paridade, onde transmissor e receptor concordam sobre a paridade a ser usada na transmissão - par ou ímpar - e, então, o transmissor acrescenta o bit de paridade para adequar o código à paridade adotada.Quando a informação chega no receptor, o processo inverso é realizado.Caso a paridade esteja incorreta, houve um erro na transmissão.
No método de paridade par, o valor do bit de paridade é determinado para que o número total de 1s na palavra código, incluindo o bit de paridade, seja par.
O método de paridade ímpar é empregado para que o número total de 1s na palavra código, incluindo o bit de paridade, seja ímpar.
Para se usar o método de paridade, transmissor e receptor definem a paridade par ou ímpar que será aplicada nas trocas de informações(protocolo). O transmissor gera e anexa o bit de paridade na palavra código e transmite; o receptor, ao receber a palavra código, analisa a paridade. Se a paridade está conforme o protocolo definido, a palavra é aceita; se a paridade da palavra recebida não está conforme o protocolo, o receptor envia uma mensagem de erro.
O método da paridade deteta apenas um erro. Ele não funciona para dois erros.

Atualizada em 13/09/17
