


Aluno:______________________________________________________ CPF Nº:___________________
1.Utilizando somente o CI multiplexador 74AS151 mostrado na Fig.1 abaixo, complemente a Fig.1B de modo que a saída Y seja igual à função lógica das variáveis de entrada t, u, v, x e Y= f(t,u,v,x) é dada por
Y = f(t,u,v,x) = Σm(0,mi,5,6,9,10,12,15)
Considere mi igual ao terceiro menor dígito do seu CPF. Mostre todas as entradas e a saída na Fig.1B.
Solução
 |
 |
|
Fig.1A |
Fig.1B |
Dígito do CPF |
mi |
Σm(0,mi,5,6,9,10,12,15) |
f(t,u,v,x) |
0 |
0 |
(0,5,6,9,10,12,15) |
|
1 |
1 |
(0,1,5,6,9,10,12,15) |
|
2 |
2 |
(0,2,5,6,9,10,12,15) |
|
3 |
3 |
(0,3,5,6,9,10,12,15) |
|
4 |
4 |
(0,4,5,6,9,10,12,15) |
|
5 |
5 |
(0,5,6,9,10,12,15) |
|
6 |
6 |
(0,5,6,9,10,12,15) |
|
7 |
7 |
(0,5,6,7,9,10,12,15) |
|
8 |
8 |
(0,5,6,8,9,10,12,15) |
|
9 |
9 |
(0,5,6,9,10,12,15) |
mi = 0
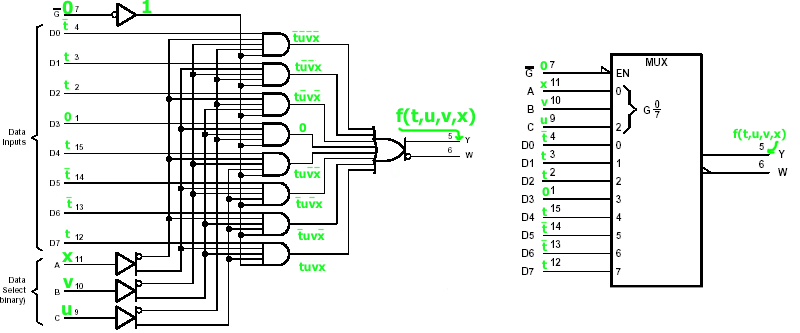 |
Fig.1 |
mi = 1
 |
Fig.1 |
mi = 2
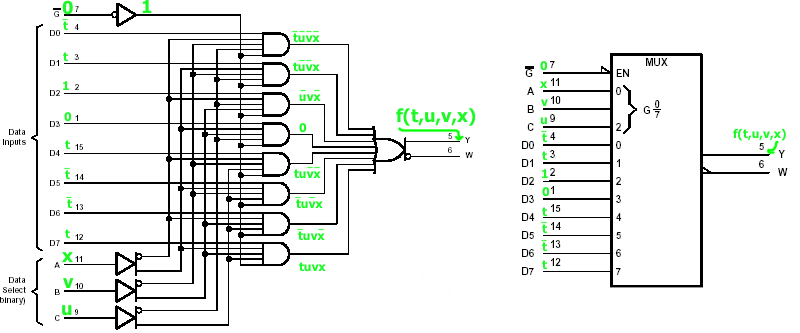 |
Fig.1 |
mi = 3
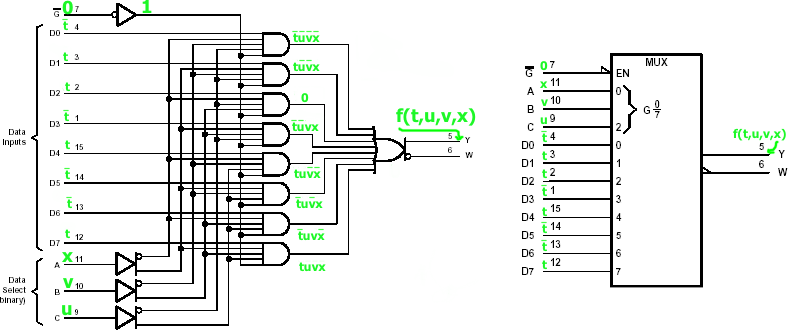 |
Fig.1 |
mi = 4
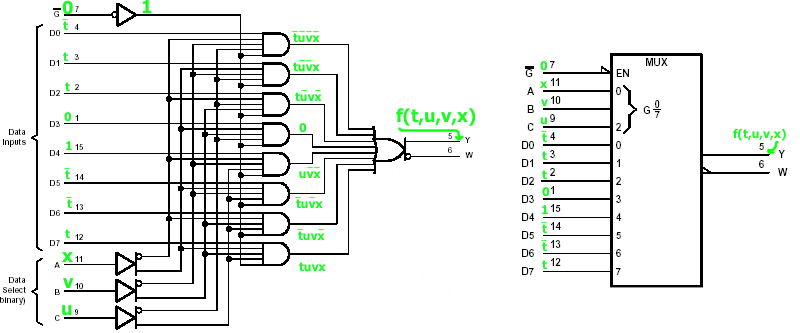 |
Fig.1 |
mi = 5
 |
Fig.1 |
mi = 6
 |
Fig.1 |
mi = 7
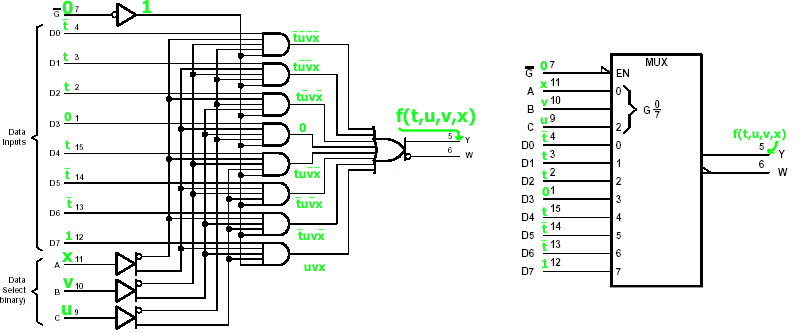 |
Fig.1 |
mi = 8
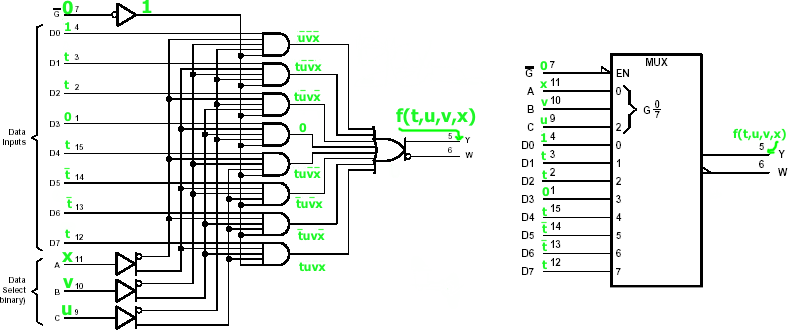 |
Fig.1 |
mi = 9
 |
Fig.1
|
Função f(t,u,v,x) correta = 2,0
Circuito da Fig.2B correto = 3,0
Valor da questão = 5,0
2.Para contador da Fig.2 abaixo, desenhe as formas de onda dos sinais de saída solicitados na figura durante 12 ciclos de clock e determine o módulo do contador. Considere que os FFs estão inicialmente com a representação BCD do segundo maior dígito do seu CPF.
Solução
Observe que os flip-flops A e B formam um contador módulo 3 com estados de contagem iguais a
BA=00→01→10→00→...
pois quando, em curto intervalo de tempo, BA=11, os flip-flops A e B são reset, desde que as entradas CLR são colocadas em 0 pela saída da porta NAND cujas entradas são BA=11.
Agora, veja que o flip-flop C é um contador módulo 2 com estados de contagem iguais
C=0→1→0...
Então, os flip-flos C, B e A formam um contador assíncrono com módulo igual a 6.
b)Então, do exposto acima, os estados de contagem do contador CBA são iguais a
CBA=000→001→010→100→101→110→000→...
As formas de onda para A, B, e C estão mostradas abaixo e as resposta corretas correspondentes para o complemento de A e complemento de B.
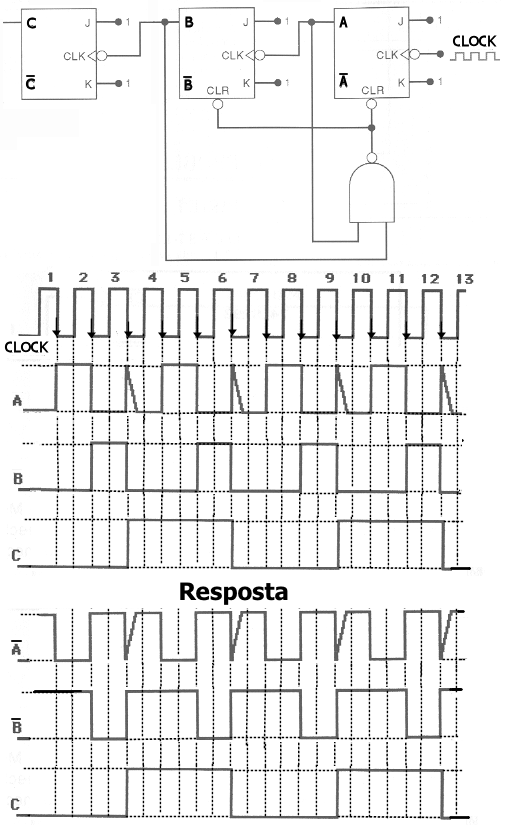
Fig.2
Valor da questão = 5
Cada forma de onda correta = 1,0
Módulo correto = 2,0

Atualizada em 22/09/23
